小3（新小4） 小4算数トップレベル講座
算数好きのこどもたちが集う最高レベル講座
4月～7月実施
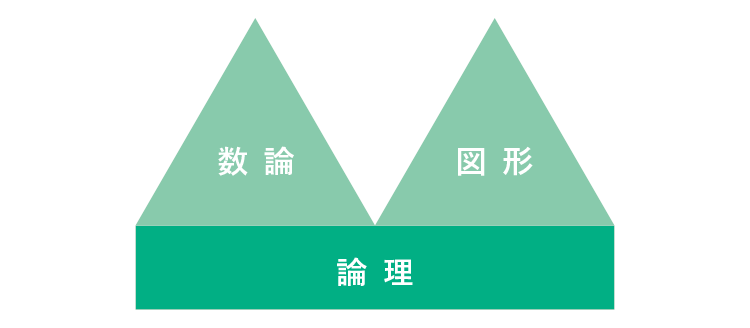
「数論」と「平面図形」を題材に技術の習得､
技術の適正な運用方法の学習を行います
なぜ2つの単元に絞るのか。
例えば男子最難関中を見ると､筑波大附属駒場中の最近10年間の「数論」と「平面図形」の出題割合は80％を超えています。
これは開成中でも同様です。さらには､算数の最高峰ともいえる算数オリンピックでは､論理､数論､図形の出題がほぼ100％となります。文章題と異なり､その場での判断力､これまでの学習経験が大きく力の差となって表れることが背景にあるでしょう。
そして子どもたちに最も楽しんでいただきたい内容だからこそです。
土台を支える「論理」
「図形が苦手です」こういったご相談をいただきます。本格的な平面図形が始まるのは4年生からであることを考えると4年､5年で図形が苦手という考え方は少し時期尚早と感じますが､苦手と勘違いされる原因としては､公式を覚えても正解に至ることができるかは別問題だからです。正解に至るためには､公式をいかに使えるようにしていくか､つまり運用能力に関わります。それがまさに「論理」です。小4算数トップレベル講座では､カリキュラム学習ではなかなか扱いきれない「論理」の問題を必ず扱います。
知識をつけることよりも､「なぜ」そうなるのかを考えて欲しい
「各位の和が3の倍数であればその数は3の倍数…。なぜ！？」
例えば「9の倍数判定法…各位の和が9の倍数であればその数は9の倍数」を説明できる“受験生”はどれくらい存在するのでしょう。
3桁の整数ABCで説明すると､ABCを「桁ばらし」という技術を用いて表現するとABC＝A×100＋B×10＋C×1となります。
この式をA×（99＋1）＋B×（9＋1）＋C×1＝A×99＋B×9＋A＋B＋Cとさらに変形するとA×99＋B×9はすでに9の倍数ですから残りのA＋B＋Cが9の倍数であればABCは9の倍数となります。このように､ただ単に3の倍数判定法を知っているだけではただの物知りで､今の最難関中入試に対応しきれません。その定理はなぜ成立しているのかを証明できなければ技術を習得しているとは言えないのです。
実施要項
| 対象 | 小3（新小4）
|
|---|---|
| 受講資格 | 小4算数トップレベル講座の受講資格は以下のテストにて認定致します。 【受講資格認定テスト】 ▼4月～7月実施分の講座受講資格
▼6月・7月実施分の講座受講資格
▼7月実施分の講座受講資格
|
| 日程 |
|
| 時間 | 9:30～11:30 |
| 科目 | 算数 |
| 実施校舎 | |
| 受講料 | 1講座 5,000円
|
| 持ち物 | ノート・筆記用具 |
| 備考 |
|
| 申込方法 | 3/27（木）10:00よりお申し込み受付を開始致します。 |
| 申込締切 | 【4月分】4/3（木）19:00 【5月分】4/17（木）19:00 【6月分】5/22（木）19:00 【7月分】6/19（木）19:00 |
関連コースのご案内
